Humans: Pattern Matching Machines?

I have a personal maxim (or apothegm, to use a word I just learned) which states, “two isn’t a pattern, and three barely is”. My purpose for reminding myself of this message is the quell the natural human tendency to assume there is an underlying pattern to something when there really isn’t enough evidence to assume so.

Consider an event with two possible outcomes (formally known as a ‘Bernoulli trial’), for instance: will the weather tomorrow be hot or cold? Obviously this is a simplification of temperature, but humans do think in such simplifications. If yesterday’s weather was hot and today’s weather is hot, what do we expect tomorrow’s weather to be like? Hint: not cold. We see the first two hot days and—Aha!—(we think) we see a pattern. But does it really exist?

A useful way to get at this problem is to consider a completely random event, like the flip of a fair coin. By definition, something which is random does not have an underlying pattern, so we can compare the flip of our fair coin to events like simplified weather prediction and see how similar (or dissimilar) they are.

Let’s flip a coin twice. Here are the possible outcomes:

1. HH
2. HT
3. TH
4. TT

I’ll define the term patternness to describe an outcome has the appearance of being caused by an underlying pattern. Which outcomes exhibit patternness here? Outcomes 1 and 4. So 2 of 4, or 50%, of the trials exhibit patternness. But recall that this is a random event, so there is no underlying pattern. To synthesize, even though there is no underlying pattern, the outcomes suggest a pattern 50% of the time.

This should shed some light on the original statement that two events don’t constitute a pattern. Even if it looks like there is a pattern, the odds of there actually being one are equal to the odds of there not being one¹. We really don’t know anything at all.

Now let’s examine a series of three coin flips. Possible outcomes:

1. HHH
2. HHT
3. HTH
4. HTT
5. THH
6. THT
7. TTH
8. TTT

This time we see patternness in 2 of 8 outcomes, or 25%, of trials of our fair coin flip. Notice that we find a lot less patternness in the three coin flip. This is what we would expect; by adding more outcomes we are suppressing the influence of the coincidental, pattern-looking outcomes on our probability.

Still, if we find ourselves looking at an HHH or TTT (three-in-a-row)-style outcome in our lives, we’d do well to remember that even a completely random coin flip would produce such a “coincidence” a whole 25% of the time.

But why are we so prone to over-detect patterns? I conjecture the reason is that humans are pattern-matching machines. We’ve evolved highly-specialized cognitive equipment for the detection of patterns because identification of patterns gave our ancestors a vast advantage in the game of survival and reproduction². In fact, pattern recognition is the foundation of much (most?) learning. Pattern recognition let our ancestors know that predators were dangerous and that bitter-tasting plants were likely poisonous (e.g. hemlock). And we find that in most of these cases, over-detection of patterns is far less harmful than under-detection. In other words, it works well to err on the side of assuming the existence of a pattern because the alternative could mean death.

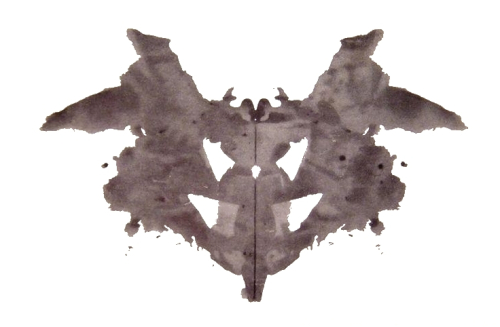
The perception of patterns where they really do not really exist is known as apophrenia³ (from Gk. apo- “off of or away from” +phren- “mind” +ia). Probably the most accessible instances of pattern over-detection are visual, where they are known as pareidolia. Pareidolia is the reason people see the virgin mary in a grilled cheese sandwich and Satan’s face in the smoke of the crumbling WTC towers. It’s why we can see faces and animals in cloud formations, and we can’t help but find some pattern in a Rorschach inkblot. It seems to me quite unsurprising that the most common interpretations of these abstract images seem to be faces, humans, and other animals—all of which would be important to primative human survival.

Of course the detection of these patterns does us no good if we don’t apply them. When we run across something new we cross-check it against our internal list of known patterns, and we develop a set of assumptions. Another word for this pattern application is stereotyping, a word which has unfortunately been vilified due to the existence of potentially-harmful types of stereotyping like sexism and racism. We would do well to watch how we use our words and where we place our emotional emphasis, however, because even these words might not be the real culprits. Stating that women and men differ physically is literally sexism, and that Caucasians have “white” skin is literally racism; sexual and racial prejudices are the actual concerns.

I’ve wandered far from my original topic, but in summary, always recall that you are hard-wired (wet-wired?) to find and apply patterns, and whether weather or gender is your topic, you might need to keep this mechanism in check to arrive at the right conclusion.